The Astrologer Experiment
A couple of days ago I came across a Youtube video which got me thinking. The channel was called Cut and the video in mind: An Astrologer Guesses Strangers' Zodiac Sign - a video containing pseudoscience and guessing! The premise is quite simple: the persons in charge of the channel have invited an astrologer and a line-up of twelve persons, one of each astrological sign, and asked the astrologer to correctly assign an astrological sign to each person in the line-up. The astrologer is free to ask the participants questions about their lives in general and to study them and their responses. Furthermore the astrologer is only given twelve cards with the astrological signs, one for each sign, meaning that a sign can be only assigned to one person. However, the astrologer is free to change his mind during the experiment and switch around the signs until he believes he has found the right matches.
The experiment has its run and in the end the participants wearing the correct sign are asked to raise their hands. The astrologer gets four out of twelve correct matches. Some questions immediately came to mind: how likely is it get $4 \over 12$ correct answers, or how likely is to get $n \over 12$ correct answers for that matter, and how many correct matches will there be on average? (All given that the guesses are completely random.)
Let's start with the number of ways to arrange all the signs. At the start the first sign can be given to any of the twelve persons: $12$ choices. The next sign can be given to one of the $11$ remaining persons. This means that for the two first assignments we have $12 \cdot 11$ possible ways to do it. The pattern repeats for the remaining signs:
$$12 \cdot 11 \cdot 10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 12! = 479 001 600.$$
So a lot of possible ways to arrange the signs, but how likely is it to get $4$ correct matches? To get the probability we need know how many ways there are to arrange the signs so that exactly $4$ signs end up with the correct person. This involves calculating the partial derangement. A mathematical derangement is how many ways the elements can be arranged so that no element end up in the correct position. In our case we want to have some signs in the correct place while the others does not matter as long as they are in the wrong place. This is known as a partial derangement and to help us with this we have recontres numbers. They are written as $D_{n,k}$ for $n$ permutations and $k$ fixed points. For our example we have $n = 12$ and $k = 4$. The recontres number are calculated recursively as
$$D_{n,k} = {n \choose k} \cdot D_{n-k,0}$$
with the recontres numbers for $k = 0$ given as
\begin{align}
&D_{0,0} = 1, \\
&D_{1,0} = 0, \\
&D_{n+2,0} = (n + 1)(D_{n+1,0}+D_{n,0}). \\
\end{align}
A long computation but here it is for our case: $D_{12,4} = 7 342 335$. This gives us the probability
$${D_{12,4} \over 12!} = {7 342 335 \over 479 001 600} \approx 0.015.$$
So the probability for the astrologer to get $4$ correct answers is $1.5 \%$. The probability is not incredibly low (it is not one in a million), but it is not high either (unlikely outcome for a single experiment). I took the liberty to calculate the values for $3, 2, 1$ and $0$ correct answers as well:
\begin{align}
3&: 0.061 \\
2&: 0.184 \\
1&: 0.368 \\
0&: 0.368. \\
\end{align}
Here we see that getting three correct answers is over $1 \over 20$ and getting two correct answers could happen almost every fifth time the experiment is performed. Still $1.5 \%$ is low but there is more at play here. Firstly, the astrologer's choices weren't completely random like we assumed above. He could see the participants reactions when he assigned them a sign and he had the possibility to change his mind afterwards. Then secondly the persons knew which astrological sign they were. So if we assume that a person willing to participate in an experiment regarding astrological signs have some interest in astrology and know what is commonly expected of their sign, they might just act like it when they meet an astrologer and answer his questions subjectively. This takes us away from complete randomness and we need to alter the model.
I have written a small Python script to simulate the experiment. As the signs are all unique, as are the participants, the problem boils down to arranging the signs in the correct order, or for the sake of simplicity, arranging numbers in an array. So to simulate the experiment the scripts take a sorted array and shuffles it, corresponding to a completely random assignment of the signs. Then to add the human factor the I introduce a human factor probability that describes how likely a wrongly placed sign is to switch back to its correct place before locking in the answers. With at human probability factor of $0.0$ the the expected outcome is the same as the calculation from above. Here is a plot from the simulation with $100 000$ iterations of the experiment:
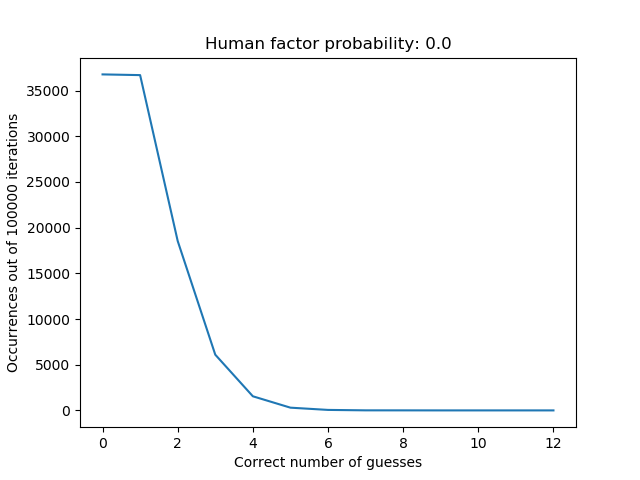
So for $100 000$ iterations we expect $1 500$ ($1.5 \%$) runs to end up with $4$ correct guesses. And it seems like we did. This goes for $3$, $2$, $1$ and $0$ correct guesses as well. The average of number of correct guesses for the $100 000$ iterations is about $1$. By some trial and error I could increase the average to about $4$ by increasing the human factor probability to $0.28$:
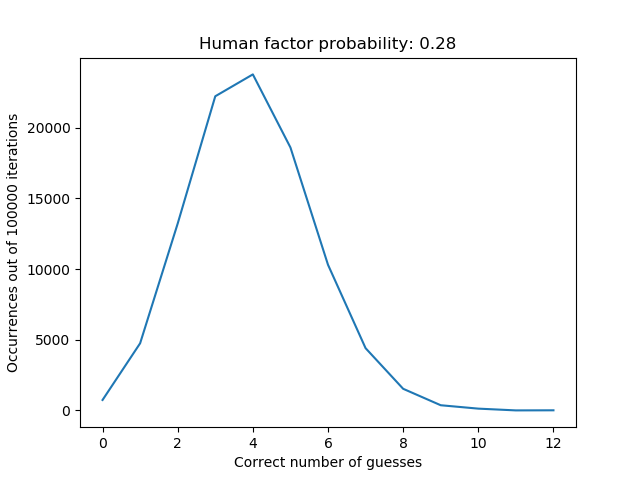
This means that if there is a $0.28$ probability for the contestant to change the astrologers mind so that the astrological sign end up in the correct place, getting $4$ correct guesses is actually the most likely outcome.
Python script: astrologer.py